"Bayesian Meta-Learning for the Few-Shot Setting via Deep Kernels" (NIPS 2020) - M Patacchiola et al.
Meta-learning 은 new task의 적은 데이터를 빠르게 학습시켜 test 데이터를 잘 맞추고 싶을 때 사용하는 알고리즘이다. 대표적인 방법으로 gradient based meta learning의 MAML이 있다. 이번 논문은 gaussian process를 사용한 model-based meta learning 방법이다. neural process는 gaussian process를 흉내 낸 방법인 반면 이 논문은 직접 사용한다는 차이점이 있다.
Introduction
MAML과 같은 gradient-based meta learning의 방법은 inner loop와 outer loop가 존재한다. inner loop 에서는 task 별 adaptation을 시행하고 outer loop에서는 meta update를 진행한다. 이런 방법은 new task가 들어왔을 때 적은 데이터로 빠르게 adaptation 하여 좋은 성능을 내는 point를 찾아준다. 하지만 2번 미분을 구해야 해서 training 시간이 오래 걸린다는 치명적 단점이 존재한다. 그래서 이 논문에서는 inner loop를 gaussian process를 사용하여 대체하고자 한다.
Method
알고리즘은 다음 표와 같다.

이 논문에서 제시하는 방법은 간단하다. task-common parameter $\phi, \theta$를 training시 optimize한다는 것이다.
그럼 어떻게 task-specific 한 문제를 맞추나에 대한 문제가 생긴다. 이를 해결하기 위해 inner loop를 gaussian process로 대체하고 task에 대한 파라미터 $\rho$를 marginalize 하는 것이다.

이렇게 하면 inner loop를 따로 두지 않아도 되어 빠른 학습이 가능해진다.
간단히 정리하면, 학습시에는 kernel에 대한 hyper-parameter와 neural network를 task-common 하게 학습하고 test 시에 new data $T^{x}_{*}$을 사용하여 gaussian process regression으로 posterior 분포를 찾게 하는 것이다. gp 특성상 kernel function을 뭘 쓸지를 잘 정하는 게 중요한 문제가 된다.
Experiments
본래 MAML이나 기타 variants들은 regression에서 별로 좋은 성능을 보이지 않는다. 하지만 이 논문의 방법은 kernel을 사용한 gaussian process를 사용하므로 상당히 smooth하고 예쁜 curve를 만들어낸다 (물론 좋은 kernel을 쓸 경우에).

meta learning 논문 실험에 자주 등장하는 sin 곡선에 대한 실험과 head trajectry estimation 실험이다. Deep Kernel Transfer (DKT)가 이 논문에서 제시한 방법의 결과다. (a) 결과를 보면 상당히 잘 맞춘 결과를 볼 수 있다. 다만 RBF kernel는 smooth 하지만 fitting이 잘 되어 있지는 않은 반면 Spectral kernel은 잘 맞췄다. 사실 Spectral kernel 자체가 cos term이 들어가기 때문에 주기 함수를 맞추는데 유리하기 때문인 것 같다. 반면 (b)는 RBF로 괜찮은 성능을 보인다. gp 특성상 uncertainty까지 보여주니 상당히 좋아 보인다.
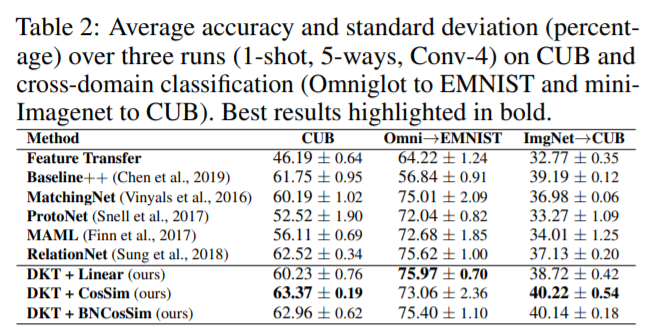
classification도 기존 알고리즘보다 좋은 성능을 보였다고 하는데 여기서도 kernel dependency가 큰 것 같다. 이런 면에서는 neural process 계열이 더 편한(?) 알고리즘이라 할 수 있을 것 같다.