simpling

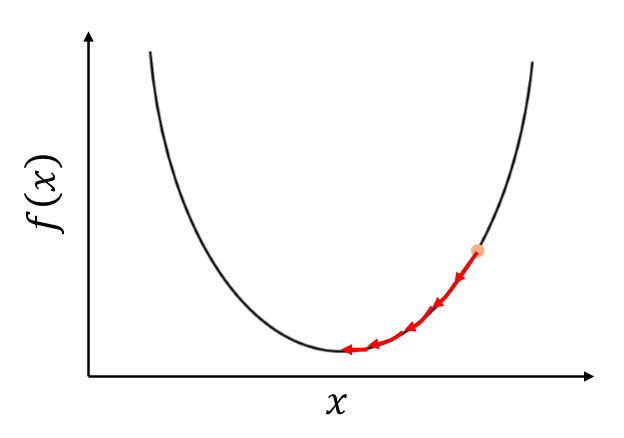
이번에는 경사하강법을 이용해 최적화를 할 때 Learning Rate(학습률)을 사용하는 이유를 알아 볼 것이다. 경사하강법은 이전 글에서 작성한 것처럼 Loss값을 줄이는 과정으로 파라미터를 업데이트하는 과정인데 이를 수식으로 작성하면 다음처럼 표현할 수 있다. $L(\theta+\Delta \theta) < L(\theta)$ 위의 조건의 만족되면 Loss가 계속 줄어가는 것이니 학습이 잘 되는 것이다. $L(\theta+\Delta \theta)$ 를 Taylor 정리를 사용하면 다음과 같이 나타낼 수 있다. $$L(\theta+\Delta \theta) = L(\theta) + \bigtriangledown L * \Delta \theta + \frac{1} {2}\bigtriangledown^{..

인공지능 모델의 전체적인 과정을 보면 다음과 같다. 데이터 입력 => 파라미터(weight, bias)를 통한 output 도출 => loss값 생성(label값과 prediction값의 차이 이용) => loss를 줄기 위해 기울기를 이용한 최적화(경사 하강법 적용, parameter 갱신) * loss를 구하고 경사하강법을 적용하는 것이 모델 학습의 핵심이다. 파라미터 weight과 bias를 이용하여 x를 input으로 주었을 때, H(x)=Wx+b의 output을 내게 된다. 이때 H(x) 값과 Label값을 비교하여 Loss를 생성한다. 대표적인 Loss 함수 Mean Squared Error를 이용한다고 했을 때, 식이 다음과 같다. MSE = Mean((H(x)-Label)^2)/2 = Me..