"Learning towards Minimum Hyperspherical Energy" (2018, NIPS) - Liu et al.
이 논문은 효율적인 neural network 학습을 위해 서로 다른 neuron이 나타내는 feature 사이의 distance가 증가하게 하고 그로 하여금 generalization 성능을 이끌어 내려고 한다.
Introduction
최근 Neural Network 관련 paper들을 보면 크면 클수록(over parameterization) 잘 된다라고 한다. 그런데 한편으로는 클수록 correlation이 높은 neurons가 많아서 redundant 하다고도 한다. 그래서 큰 모델을 학습시키고 Pruning을 시켜 compression 하는 방법이나 efficient network를 찾는 방법을 사용한다. 이 논문에서는 training 할 때 neuron 간의 correlation을 낮춰 redundant한 neuron을 줄이고 generalization을 이끌어 내고자 한다.
논문의 제목에서도 알 수 있듯이 Hypershperical energy를 minimize 하여 목표를 달성하고자 한다. Energy는 아래 Formulation에서 정의하는 것을 보면 알 수 있고, 높은 energy를 가질수록 redunancy가 높아지고 낮은 energy일수록 neuron이 다양하고 유니폼하게 위치하여 낮은 energy를 가진다고 생각할 수 있다.
Formulation
Energy는 아래 1번식 처럼 표현한다.
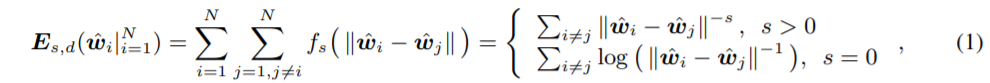
하나의 layer에 N개의 neuron이 있고 각 weight는 d+1 dimension을 가질 때의 상황이다. $f_{s}$는 decreasing real-valued function이며 뭘 쓸지는 선택할 수 있는데 이 논문에서는 $f_{s}(z) = z^{-s} (s>0)$ 를 사용한다. $\hat{w_{i}}$ = $\frac {w_{i}} {||w_{i}||}$ (unit hypersphere에 projection된 neuron)
위의 식을 간단히 해석하면 각 neuron의 distance가 클수록 Energy는 감소하게 된다고 볼 수 있다 ($f_{s}$ 가 decreasing function 이므로).
Energy를 minimize 하는 식은 아래 2번식(s=0인경우),3번식(s>0인 경우) 과 같이 나타낼 수 있다.
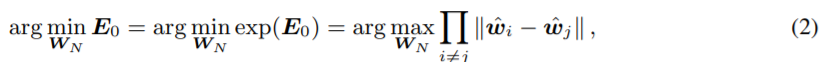
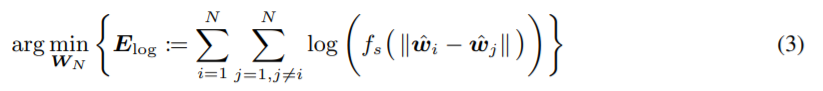
Loss object는 아래와 같다.

MHE Variants
MHE의 변형으로 논문에서 제시한 것이 있다.
1) Half-space MHE
figure2의 왼쪽 그림을 보면 그냥 MHE를 사용했을 때 neuron의 방향은 반대이나 (그래서 distance는 크지만) collinear한 관계가 되버린다. 이런 경우를 방지하기 위해 half-space MHE를 제시한다.

방법은 간단한데, 애초에 반대방향의 neuron을 생성하고 MHE를 사용하는 것이다. 그러면 결과적으로 (원래 N개의 neuron이 존재하면) 2N개의 neuron을 얻게 될 것이고 이는 Figure 2의 오른쪽 그림처럼 correlation이 낮은 $\hat {W_{1}}, \hat {W_{2}}$를 얻을 수 있게된다.
하지만 실제로 high-dimensional space 에서는 collinearity가 거의 일어나지 않으므로 그냥 MHE 방법도 잘 된다고 주장한다.
2) Angular MHE
(1)번 식에서는 원래 Euclidean distance로 neuron간의 거리를 구했는데 이번엔 (5)번 식처럼 arccos (angle)을 사용한다.
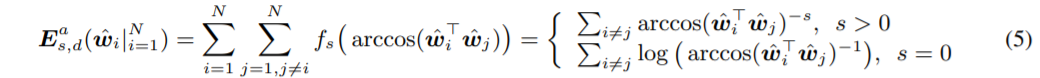
이는 unit hypersphere에서 neuron 사이의 각도로 나타낸 거리가 커지게 만든다.
Experiments
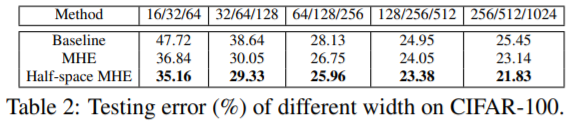
흥미로운 실험들만 남겨둔다. Table2는 width가 커질 때 각 알고리즘 결과이고 Table3은 depth가 커질 때 결과이다. MHE를 썼을 때 Baseline 보다 network size가 작음에도 (width, depth 모두) 더 좋은 성능을 보이는 경우가 많았다.

서로 다른 classifier neuron에 대해서도 hyperspherical margin이 maximize 되도록 학습되어서 Class Imbalance 문제에서도 잘 작동했다. Figure4는 MNIST 데이터에서 0에 해당하는 데이터를 98% 날리고 학습시켰을 때 결과다. (화살표는 classifier neuron이고 각 색에 해당하는 것은 숫자다)
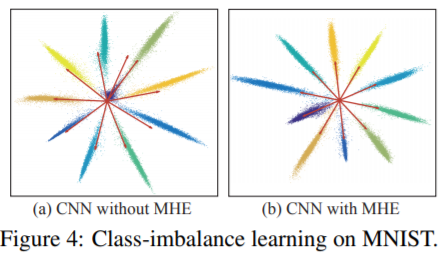
왼쪽이 MHE를 안쓴 경우인데 남색(아마 0에 해당하는 듯) 부분 화살표를 잘 보면 연두색과 매우 가깝고 제대로 분류하지 못한 것을 볼 수 있다. 반면 MHE를 쓴 오른쪽은 남색도 clear 하게 분류한 것을 볼 수 있다.