https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians
https://namu.wiki/w/%EA%B0%80%EC%9A%B0%EC%8A%A4%20%EC%A0%81%EB%B6%84
https://mathcs.clarku.edu/~djoyce/ma217/contexp.pdf
https://ko.wikipedia.org/wiki/%EC%A0%95%EA%B7%9C_%EB%B6%84%ED%8F%AC
이번에는 두 개의 서로 다른 Gaussian 분포를 가정했을 때 KL-divergence(Kullback–Leibler divergence, KLD)를 구하는 유도 과정을 정리한다. 위의 여러 링크들을 참고하였는데 중간중간 생략한 내용들이 많아 자세한 설명을 남겨둔다.
먼저 알아둬야 할 기초적인 내용을 정리해 보겠다.
1) Gaussian 분포
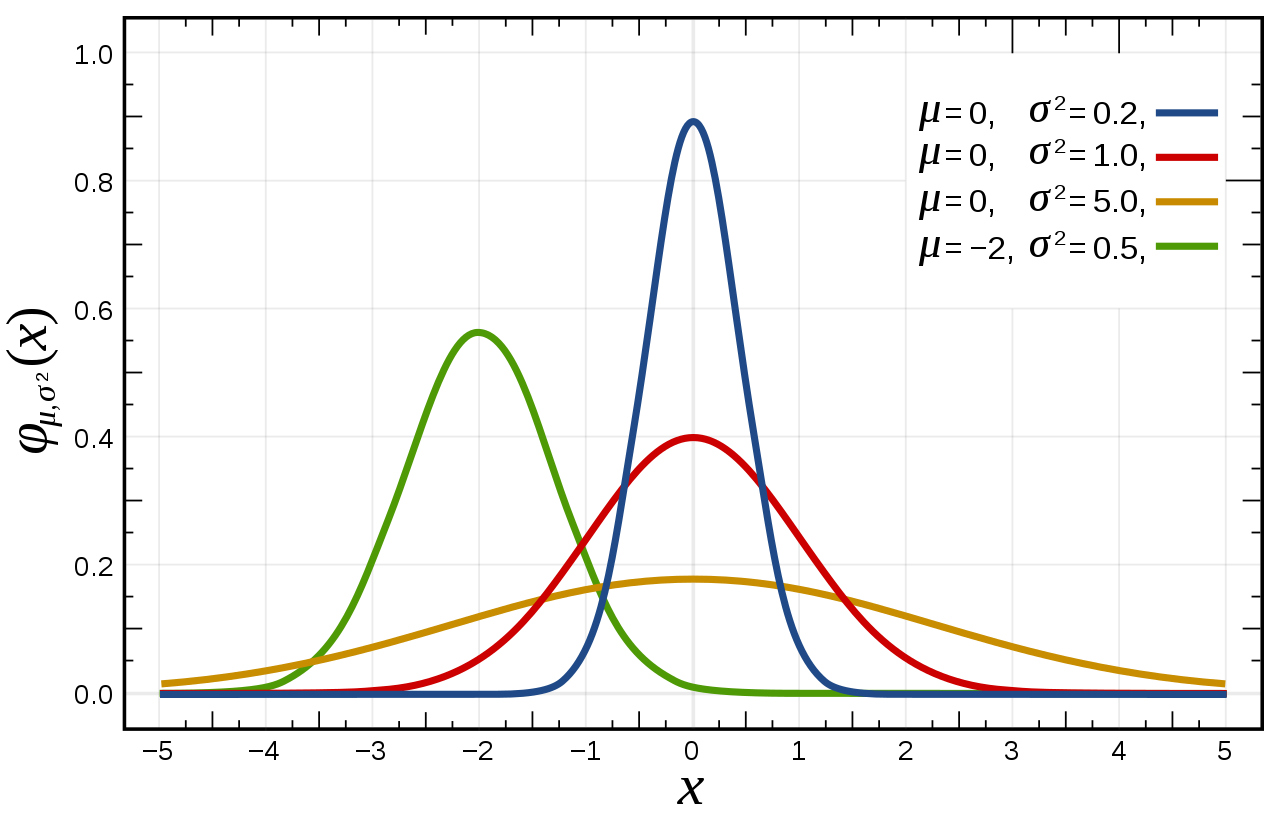
가우시안 분포는 위의 그래프와 같이 mean과 variance에 따라 다른 모양을 가진다. 빨간색 그림처럼 mean=0, variance=1 인 경우를 특별히 표준 정규 분포라고 부른다.
$mean : \mu, variance : \sigma^{2}$인 가우시안 분포를 함수로 나타내면 아래의 수식과 같다.
$$ N(\mu, \sigma) = \frac {1} {\sqrt {2\pi \sigma^{2}}} e^{\frac {-(x-\mu)^{2}} {2 \sigma^{2}}} \cdots (1)$$
2) 기댓값(평균값)
밑에서 기댓값에 대한 내용이 나와 간단히 정리하고 넘어간다. 고등학교 통계학 때 배운 내용으로 매우 기초적인 것들이다. 기댓값은 평균값과 같은 의미로 사용되며 discrete random variable X에 대한 식은 다음과 같이 표현된다.
$$ \mu = E(X) = \sum_{x} xf(x) $$
| x | 0 | 1 | 2 |
| P(x) | 1/4 | 1/2 | 1/4 |
이에 대한 간단한 예시로 위의 표와 같은 값을 갖는 x와 그에 대한 확률 P(x)가 있을 때 평균값은 다음과 같다.
$$ \mu = 0 * \frac {1} {4} + 1 * \frac {1} {2} + 2 * \frac {1} {4} = 1 $$
다음으로 continuous random variable X에 대한 식은 다음과 같이 표현된다.
$$ \mu = E(X) = \int_{-\infty}^{\infty} xf(x) dx \cdots (2) $$
discrete 한 값을 계산하는 것에서 적분식으로 바꿔준 것으로 만약 [a, b] 구간을 벗어난 f(x) 값이 0이라면 다음과 같이 표현할 수 있다.
$$ \mu = E(X) = \int_{b}^{a} xf(x) dx $$
(기댓값과 관련한 내용은 여기를 참조)
3) 가우스 적분
유도 과정에서 가우스 적분이 필요하기 때문에 먼저 정리해둔다. (정확한 유도과정은 여기를 참조)
$$ \int_{-\infty}^{\infty} e^{-x^{2}}dx = \sqrt {\pi} \cdots (3) $$
$$ \int_{-\infty}^{\infty} x^{n} e^{-ax^{2}}dx = \frac {2(n-1)!} {2^{(n+2)/2} a^{n/2}} \sqrt {\frac {\pi} {a}} (n:짝수) \cdots (4)$$
$\cdot$ Kullback–Leibler divergence with Gaussian distribution
KL-divergence(KLD)는 두 확률 분포 사이의 차이가 얼마나 나는지를 보기 위한 함수다. 두 확률분포 p, q에 대한 KLD를 식으로 표현하면 다음과 같다.
$$ D_{KL}(p||q) = \int p(x) log \frac {p(x)} {q(x)} dx $$
$$ = \int p(x) log p(x) dx - \int p(x) log q(x) dx \ge 0 $$
두 함수의 분포가 같아지면 $D_{KL} (p||q) = 0$이 된다.
이제 p와 q가 Gaussian 분포를 따른다고 가정하고 식을 유도해 볼 것이다. p $ = N(\mu_{1}, \sigma_{1}) $, q $ = N(\mu_{2}, \sigma_{2}) $
$$ KL(p, q) = -\int p(x) log q(x) dx + \int p(x) log p(x) dx $$
1) $ \int p(x) log p(x) dx $ 계산
먼저 $\int p(x) log p(x) dx$에 대해 계산해본다. 편의상 $ Z = \frac {1} {\sqrt {2\pi \sigma^{2}}} $으로 나타낸다. p에 대한 분포이므로 $\sigma_{1}, \mu_{1} $에 대한 식이지만 여기서는 구분하지 않아도 되므로 생략한다.
(1)의 gaussian 함수를 p(x)에 넣으면 다음과 같이 정리된다.
$$ \int p(x) log p(x) dx = \int Z e^{-\frac {(x-\mu)^{2}} {2 \sigma^{2} } } (- \frac {(x-\mu)^{2}} {2 \sigma^{2}} +log Z) dx $$
이제 $\frac {x-\mu} {\sqrt {2}\sigma} = t, \frac {1} {\sqrt {2} \sigma} dx = dt$ 로 치환하면 다음과 같다.
$$ \int Ze^{-t^{2}} (-t^{2} + log Z ) \sqrt{2} \sigma dt $$
Z를 다시 바꾸고 괄호를 풀면 다음과 같다.
$$ \frac {1} {\sqrt {\pi}} \int e^{-t^{2}} (-t^{2}) dt -\frac {log(2\pi \sigma^{2})} {2 \sqrt{\pi}} \int e^{-t^{2}} dt $$
여기서 가우스 적분식 (3)과 (4)를 이용하면 최종적으로 다음과 같이 유도된다.
$$ \int p(x) logp(x) dx = - \frac {1} {2} - \frac {1} {2} log(2 \pi \sigma_{1}^{2}) = -\frac {1} {2} (1+log(2\pi \sigma_{1}^{2})) $$
2) $ \int p(x) log q(x) dx $ 계산
다음으로 $ \int p(x) logq(x) dx $를 계산해본다. 먼저 (1)의 gaussian 함수를 q(x)에 넣어 정리한다.
$$ - \int p(x)logq(x) dx = - \int p(x) log \frac {1} {\sqrt {2 \pi \sigma_{2}^{2}}} e ^{-\frac{(x-\mu_{2})^{2}} {2\sigma_{2}^{2}}} dx $$
log안의 식을 분리하면 다음과 같다.
$$ - \int p(x) log \frac {1} {\sqrt {2\pi \sigma_{2}^{2}}} dx + \int p(x) \frac {(x-\mu_{2})^{2}} {2\sigma_{2}^{2}} dx $$
$ \int p(x) dx = 1 $을 사용하여 첫 번째 항을 바꾸고 두 번째 항을 전개하면 다음과 같다.
$$ \frac {1} {2} log(2\pi \sigma_{2}^{2}) + \frac {\int p(x) x^{2} dx - \int 2 \mu_{2} x p(x) dx + \mu_{2}^{2} \int p(x) dx } {2 \sigma_{2}^{2}} $$
이제 (2)의 식을 이용하여 오른쪽 항의 분자식을 바꿔주면 다음과 같다.
$$ \frac {1} {2} log (2\pi \sigma_{2}^{2}) + \frac {E_{1}(x^{2}) - 2 \mu_{2} E_{1}(x) + \mu_{2}^{2}} {2 \sigma_{2}^{2}} $$
분산의 정의가 $ \sigma^{2} = E(x^{2}) - E^{2}(x) $이므로 $ E(x^{2}) = \sigma^{2} + E^{2}(x) $을 이용하여 식을 바꾸면 다음과 같다.
$$ \frac {1} {2} log(2 \pi \sigma_{2}^{2}) + \frac { \sigma_{1}^{2} +\mu_{1}^{2} - 2\mu_{2}\mu_{1} + \mu_{2}^{2} } { 2 \sigma_{2}^{2} } $$
$$ = \frac {1} {2} log (2 \pi \sigma_{2}^{2}) + \frac {\sigma_{1}^{2}+(\mu_{1}-\mu_{2})^{2}} {2\sigma_{2}^{2}} $$
3) 정리
이제 $\int p(x) logp(x) dx$와 $- \int p(x) log q(x) dx$를 합해서 식을 정리하면 다음과 같다.
$$ \therefore KL(p, q) = - \int p(x) log q(x) dx + \int p(x) log p(x) dx $$
$$ = \frac {1} {2} log (2\pi \sigma_{2}^{2}) + \frac {\sigma_{1}^{2} + (\mu_{1} - \mu_{2})^{2}} {2\sigma_{2}^{2}} - \frac {1} {2} (1+log(2\pi \sigma_{1}^{2})) $$
$$ = log \frac {\sigma_{2}} {\sigma_{1}} + \frac {\sigma_{1}^{2} + (\mu_{1} - \mu_{2})^{2})} {2\sigma_{2}^{2}} - \frac {1} {2} $$
'머신러닝&딥러닝 > 기초정리' 카테고리의 다른 글
| Likelihood, Maximum likelihood estimation 이란? (0) | 2021.08.29 |
|---|---|
| Variational AutoEncoder란? (0) | 2020.11.29 |
| Auto Encoder란? - Manifold와 차원 축소 (0) | 2020.03.29 |
| Mean Squared Error VS Cross Entropy Error (3) | 2020.03.28 |
| 경사하강법 이해(2) - Learning Rate란? (0) | 2020.03.28 |