DNN에서 Loss Function을 사용할 때 아래의 2가지 가정에 적합해야 한다.
1) Train data에서의 Loss 총합은 개별 데이터 Loss의 합과 같아야 한다.
$$L(\theta_{k}, D) = \sum_{i}L(\theta_{k} ,D_{i})$$
2) DNN 출력 값으로 Loss를 계산한다. (중간 단계에서의 값으로는 계산하지 않음.)
$$\bigtriangledown L(\theta_{k},D) = \sum_{i}\bigtriangledown L(\theta_{k}, D_{i})$$
Mean Squared Error(MSE)와 Cross Entropy Error(CEE)를 Loss Function으로 많이 사용하는 이유는 위의 두 조건을 만족하는 대표적 함수이기 때문이다. 이번 글에서 두 함수의 차이를 알아볼 것이고 각각 Regression, Classification에 적합함을 보일 것이다.
각각의 Loss function 식은 다음과 같다. $$MSE=\frac {1} {n} \sum_{i}^{n} \frac {1} {2} (y_{i}-\tilde{y}_{i})^{2}$$
$$CEE=-\sum_{i}y_{i}log(\tilde{y}_{i})$$
($y_{i}$는 학습 데이터 정답의 i번째 요소, $\tilde{y}_{i}$는 학습 데이터 입력에 대한 예측값의 i번째 요소)
MSE의 경우는 식이 정답에서 예측한 값을 빼는 것으로 되어있어 직관적 이해가 쉽다. 하지만 CEE는 그렇지 않으므로 잠깐 알아보겠다. Cross Entropy에서 Entropy는 물리학을 배울 때 자주 나오는 단어인데 불확실성의 정도를 가리킨다. 그러므로 우리가 예측하기 힘들면 힘들수록 Entropy값은 커진다.
예를 들어, 국회의원 선거를 하는데 A후보와 B후보가 있다고 생각해보자. A후보의 지지율은 90%이고 B후보의 지지율이 10%라고 할 때,
A후보가 이기는 경우: -log(P(A)) = -log(0.9) = 0.05
B후보가 이기는 경우: -log(P(B)) = -log(0.1) = 1.0이다.
Entropy는 놀람의 정보의 평균이므로 0.9*0.05+ 0.1*1.0 = 0.15이다.
이번에는 A후보와 B후보의 지지율이 50:50이라고 생각해보겠다. 이때 각 후보의 Entropy는 0.30이다. 이때의 Entropy는 0.5*0.3 + 0.5*0.3 = 0.3이다.
계산 결과에서 보이듯 위에서 구한 값보다 아래의 경우가 Entropy가 더 높다. 즉, 확률 값이 비슷하여 예측이 힘들 때(결과가 불확실할 때) Entropy가 높게 나온다.
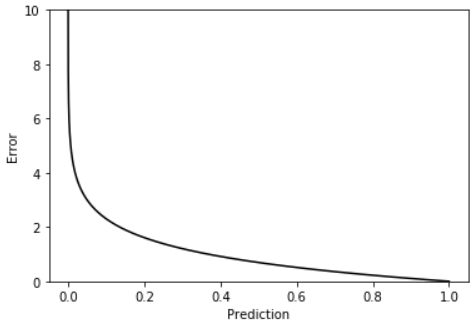
한편, Classification을 수행하는 모델에서 CEE는 정답인 클래스에 대해서 오차를 계산한다. 오차를 내는 과정에서 정답 클래스만 비교하지만, 다중 클래스 분류의 활성 함수인 softmax로 인해 다른 클래스에 대한 학습에도 영향을 준다. 위의 국회의원 예시처럼 각각의 -log(P(x)) 를 구하여 더하여 Error를 구해주는데 $\tilde{y}_{i}$ 가 0에 가까우면 가까울수록 Error는 기하급수로 커지게 된다.
두 손실 함수의 차이는 BackPropagation을 사용할 때 Loss Function에 대한 Activation Function의 미분 값을 사용하느냐에서도 나타난다. MSE의 경우 $\bigtriangledown_{a} C \odot \sigma'(Z^{L})$ 로 구하는데 CEE는 $\sigma'(Z^{L})$항을 사용하지 않아 역전파시 기울기 손실이 덜하며 속도도 더 빠르다. 그러므로 CEE는 역전파에 유리한 함수라고 할 수 있다. (하지만 중간 Layer에서는 활성 함수에 대한 미분 값을 사용하므로 결국 Gradient Vanishing이 일어나게 된다.)
Maximum-Likelihood의 관점에서 모델의 학습을 생각하면 정확한 $y$값을 찾는 것보다 $y$를 평균으로 하는 분포에 의한 파라미터(평균, 표준편차)를 찾는다고 생각할 수 있다. 이때, 2가지 가정을 하는데 다음과 같다.
1) 모든 데이터가 각각 독립적이다. $P(y|f_{\theta}(x)) = \prod_{i}P_{D_{i}}(y|f_{\theta}(x_{i})$
2) 각각의 데이터가 동일한 분포를 가진다. (ex) Gaussian분포 등등)
x는 관측된 데이터로 고정되어 있고 y를 가장 잘 설명하는 파라미터 $\theta$ 를 찾고자 하는 것이므로 $\underset{\theta}{argmax} P(y|f_{\theta}(x))$로 나타낼 수 있다. 확률값은 0~1 사이의 값을 가지므로 계속해서 곱하면 빠르게 0으로 수렴하게 된다. 따라서 log를 사용하는데 log 특성상 곱이 덧셈으로 바뀌게 된다. 이렇게 되면 위에서 설명한 Loss function의 조건을 만족시키게 된다. 또한 모델 최적화를 할 때 Maximum을 구하는 것보다 Minimize를 많이 사용하므로 Negative-Likelihood를 사용한다.
$$Loss = -log \prod_{i}(P(y_{i}|f_{\theta}(x_{i}))) => -\sum_{i}log(P(y_{i}|f_{\theta}(x_{i})))$$
이때, Gaussian 분포와 Bernoulli 분포에 대한 수식을 다음과 같이 유도할 수 있다.
$$ Gaussian-distribution $$
$$ f_{\theta}(x_{i}) = \mu_{i} , \sigma_{i} = 1 $$
$$ P(y_{i}|\mu_{i},\sigma_{i}) = \frac{1}{\sqrt{2\pi}\sigma_{i}}exp(-\frac{(y_{i}-\mu_{i})^2} {2\sigma_{i}^2}) $$
$$ -log(P(y_{i}|\mu_{i})) \propto \frac{(y_{i}-\mu_{i})^2}{2} = \frac{(y_{i}-f_{\theta}(x_{i}))^2} {2}$$
$$ Bernoulli-distribution $$
$$ f_{\theta}(x_{i}) = P_{i} $$
$$ P(y_{i}|P_{i}) = P_{i}^{y_{i}}(1-P_{i})^{1-y_{i}} $$
$$ -log(P(y_{i}|P_{i})) = - [y_{i} logP_{i}+(1-y_{i} log(1-P_{i})] $$
위 두식의 Loss는 각각 MSE , CEE 가 되는데 이에 따라 연속적 분포를 갖는 데이터(Regression) 에는 MSE가 적합하고 이산적 분포를 갖는 데이터(Classification) 에는 CEE가 적합하다고 생각할 수 있다. 하지만 딥러닝 특성상(?) 반대의 결과도 나올 수 있으며 다른 Loss Function이 적합할 때도 많을 것이므로 처음 데이터를 사용할 때 참고하는 것이 좋을 것 같다.
'머신러닝&딥러닝 > 기초정리' 카테고리의 다른 글
| KL-divergence with Gaussian distribution 증명 (0) | 2020.11.26 |
|---|---|
| Auto Encoder란? - Manifold와 차원 축소 (0) | 2020.03.29 |
| 경사하강법 이해(2) - Learning Rate란? (0) | 2020.03.28 |
| Convolution Neural Network 원리와 구조 이해 (0) | 2020.01.03 |
| 경사하강법 이해(1) (0) | 2019.12.30 |