"Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles" (ICML 2017) - DeepMind
https://www.edwith.org/bayesiandeeplearning/joinLectures/14426
기존의 연구와 한계, 해결책
딥러닝이 발전하며 많은 발전을 이루었지만 아직 부족한 것들이 많이 있다. Uncertainty를 구하는 일이 그중 하나다. 특히 의료, 금융, 자율주행 등의 task에서 overconfident 한 예측은 치명적인 결과를 이끌 수 있기 때문에 불확실성이 더욱 중요한 키워드가 되었다. 이 논문이 나오기 전에 uncertainty를 구하는 방법들은 대부분 베이지안과 관련이 되어 있었다. 베이지안 방법은 posterior 분포에 대한 mean값을 구하는 과정인데 실제로는 근사하는 방법을 사용한다.(참조) 그에 대해 간단히 설명하면 다음과 같다. input을 모델에 넣어 output을 얻을 때, 파라미터를 잘 흔들어(sampling) 연산 시마다 output이 조금씩 달라져서 확률분포처럼 보이게 하는 것을 말한다. 대표적으로 MC Dropout, MC Batch Normalization 이 있다.
한계-해결책 1) 베이지안 방법들은 훈련과정에서 많은 수정이 필요하여 computationally expensive 하며 여러 번 sampling 하는 과정이 필요하다. 그래서 논문에서는 하이퍼 파라미터 튜닝이 별로 필요하지 않고 병렬적으로 실행할 수 있으면서도 uncertainty 추정을 잘하는 non-bayesian방법을 제시한다.
한계-해결책 2) 베이지안 방법들은 여러 결과를 함께 고려한다는 점이 Ensemble과 비슷하게 보인다. 하지만 Bayesian model averaging(soft model selection)의 경우는 posterior를 잘 근사하였다고 가정하기 때문에 그렇지 않을 경우 결과가 좋지 못하다. 반면 Ensemble(model combination)은 posterior를 잘 근사하지 못해도 좋은 결과를 내며 더욱 robust 한 모델을 얻을 수 있어 논문에서는 이 방법을 사용한다.
Metrics - Scoring rules
논문에서는 Uncertainty를 측정하는 평가 방법으로 Scoring rules라는 개념을 소개하는데 이는 well-calibrate 된 예측에 대해 좋은 점수를 주고 그렇지 않으면 안 좋은 점수를 주는 지표라고 한다. 사실 대부분의 Neural Net에 대한 loss function은 적절한 scoring rules라고 한다. 여기서는 Brier Score(분류), NLL(회귀)을 사용한다. 추가적으로 Calibration Error도 나오는데 이는 이전 글에 설명이 나와있다.
텐서플로우를 사용하여 각각의 loss를 구하면 다음과 같다.
import tensorflow as tf
# output : 분류에 대한 예측값
# label : 분류에 대한 정답값
Brier Score = tf.reduce_mean(tf.div(tf.reduce_sum(tf.square(tf.subtract(output, label)), axis = 1), num_label), axis = 0)
# output_sig_pos : output으로 구한 sigma 값을 양수로 만든 값
# output_mu : output으로 구한 평균값
# label : 회귀에 대한 정답값
NLL = tf.reduce_mean(0.5*tf.log(output_sig_pos) + 0.5*tf.div(tf.square(label - output_mu),output_sig_pos)) + 5
Main contribution
논문에서 제시하는 (regression에 대한) 학습 방법은 모델의 final output으로 mean과 variance를 구하는 것이다. 보통 Network의 output이 (regression일 경우) 하나의 mean 값을 구하게 된다. 하지만 여기서는 mean과 variance를 함께 구하여 모델의 예측 분포를 알 수 있도록 하였다. 상당히 간단하면서도 신선하다. 이때 사용하는 Loss function이 (Gaussian 분포를 가정한) Negative log likelihood(NLL)이다. 논문에서 자주 비교하는 대상이 Mean Squared Error(MSE)인데 MSE는 Proper scoring rule이 아니라 predictive uncertainty를 구하지 못한다고 한다. 즉, variance를 못 구한다는 의미다. 사실 MSE는 가우시안 분포를 가정하여 regression을 수행할 때 NLL로부터 유도될 수 있다(참조). 이 경우에는 variance가 constant로 무시되어 variance term이 사라지게 되었다. 하지만 직접적으로 NLL을 수행하면 그렇지 않을 수 있어 Scoring rule에 적합하다. 식으로 표현하면 아래와 같다.
$$ -log(p_{\theta}(y_{n}|x_{n})) = \frac { log (\sigma^{2}_{\theta}(x))} {2} + \frac {(y-\mu_{\theta}(x))^{2}} {2\sigma^{2}_{\theta}(x)} + constant$$
추가적으로 모델을 잘 학습시키는 방법으로 Ensemble과 Adversarial training을 제시하였다. 여기서 말하는 Ensemble 방법은 전체 데이터 셋에서 일부를 sampling하여 각각의 모델을 학습시켜 평균값을 내주는 것을 말한다. 실험 결과를 보면 Ensemble을 하지 않은 모델과 많은 차이가 나는 것을 확인할 수 있다. Classification은 Ensemble할 때 예측값을 평균내면 된다. Regression으로 여러 모델에 대한 Mean과 Variance를 Ensemble하는 것은 mixture of Gaussian distributions에 대한 Mean과 variance를 구하는 것 이다. 그 식은 다음과 같다.
$$ \mu_{*}(x) = M^{-1}\sum_{m}\mu_{\theta_{m}}(x)$$
$$ \sigma_{*}^{2} = M^{-1}\sum_{m}(\sigma^{2}_{\theta_{m}}(x) + \mu^{2}_{\theta_{m}}(x))-\mu^{2}_{*}(x) $$
Adverarial training은 대체로 약간의 성능 개선을 이끌어 주었다. 이는 Goodfellow 교수님이 제시한 방법으로 데이터를 loss가 커지는 방향으로 perturbation 하여 실제 target의 공간을 더 열어주는 효과를 준다. 이는 예측 분포를 smooth 하게 해 줘서 더욱 robust 한 모델을 이끌어 내게 해준다. 수식은 다음과 같다. $$x' = x + \epsilon sign(\bigtriangledown_{x} l(\theta,x,y))$$
Experimentsal reults
실험 결과를 소개하기에 앞서 실험에서 MSE를 사용할 때, variance를 직접 구할 수 없으므로 empirical variance를 사용했다는 내용의 부록 결과를 소개한다.

왼쪽의 결과는 variance를 예측하여 학습한 결과를 test set에 적용한 것으로 well-calibrated 되었다. 반면 오른쪽은 empirical variance을 사용한 것으로 uncertainty를 underestimate 하는 결과를 보인다.
1. toyset으로 regression 한 결과
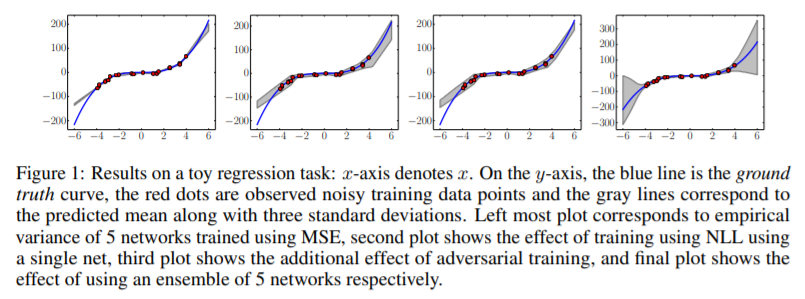
첫 번째 plot은 MSE로 훈련한 결과로 Uncertainty를 전혀 나타내지 못한다. 두 번째 plot은 1개의 모델을 NLL로 훈련한 결과로 약간의 variance를 나타내기 시작했다. 세 번째는 adversarial training을 추가한 결과로 그렇게 나은 성능을 보이진 않는 것 같다. 마지막은 5개의 모델을 앙상블 한 결과로 넓은 variance로 uncertainty를 추정하여 실제 분포를 추정해냈다. 이 실험으로 Ensemble과 Scoring rule(NLL)을 사용하는 것이 Uncertainty 추정에 좋다는 것을 알 수 있다.
2. probabilistic backpropagation , MC-dropout , Deep Ensembles 비교

RMSE를 사용하여 학습시키는 경우 논문에서 제시한 Deep Ensembles방법이 그다지 좋지 못하다. 하지만 NLL을 사용하면 대부분 더 좋은 결과를 얻음을 알 수 있다.
3. Ensemble 하는 모델을 늘려가며 여러 가지 방법을 MNIST 데이터셋과 SVHN에 적용하면 어떻게 달라지는지를 보았다.

역시 Ensemble model은 그 수가 많아질수록 모든 지표에서 더 좋은 결과를 나타냄을 알 수 있다.(이를 보여주는 다른 실험도 있으나 생략) 또한 MC dropout방법보다 Deep Ensemble 방법을 사용하는 것이 성능이 좋다. Adversarial training 방법은 augmenting with random direction 보다 좋은 성능을 내지만 Ensemble 만큼의 효과가 크지는 않다. 오히려 augmenting with random direction 방법은 Ensemble만 사용할 때보다 안 좋은 결과를 내기도 한다.
4. Uncertainty Evaluation : known VS unknown classes
사실 논문의 핵심은 이 4번째 실험이다. 학습한 데이터를 잘 구분하면서도 이상한 데이터(out-of-distribution data)가 들어올 경우 uncertainty를 높이는 것이 모델의 핵심이기 때문이다. MNIST - Not MNIST와 SVHN - CIFAR10 (왼쪽이 train, 오른쪽이 test)에 대한 실험 결과이다.
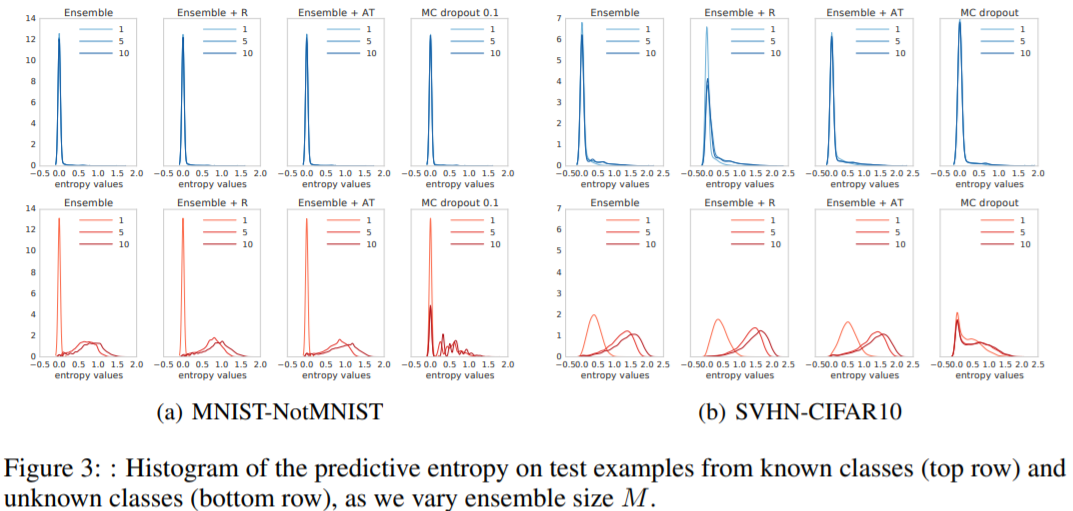
Entropy values로 측정을 하였는데 이 값이 높을수록 uncertainty 추정을 잘한 것이다. Known class(위의 그래프)에 대해서는 모든 모델이 좋은 성능을 보이고 있다. Unknwon class(아래의 그래프)는 Ensemble이 1개인 경우 entropy values가 낮지만 5개 이상의 ensemble 결과는 잘 나옴을 알 수 있다. 반면 MC-dropout은 uncertainty 추정이 Deep-Ensemble 모델보다 좋지 못하다.
정리
논문의 핵심은 2가지다. 첫 번째는 학습을 할 때, Scoring rule(NLL,BS)을 사용하여 model의 불확실성을 구하는 것. 두 번째는 그것을 Ensemble 하여 정확도를 높이는 것. 이 방법을 사용하면 기존 베이지안 방법들보다 hyperparameter tuning에 적은 시간을 사용하며 MLP, CNN 등의 다양한 구조에 사용 가능하다. 뿐만 아니라 Uncertainty 추정에 좋은 결과를 보인다는 강한 강점이 있다. 하지만 model을 여러 개 학습시켜 Ensemble 하는 방법이라 hyperparameter tuning에는 시간이 많이 걸리지 않을지라도 모델 학습 자체는 시간이 오래 걸릴 것이다. 또한 얼마 큼의 모델을 Ensemble 해야 하는지 결정하는 것도 명확하지 않다. 그래서 논문의 마지막에는 using multiple heads, snapshot ensembles, swapout의 방법을 사용해보는 것이 흥미로울 것이라고 제시한다.