DQN (Deep Q Learning [1])
DQN은 sensory input (image 등)으로부터 정책을 곧바로 배우는 첫 번째 심층강화학습 모델이다. 그만큼 강화학습 분야에서 근본이 되는 논문이다. 여러 방법을 사용해서 기존에 있던 문제들을 해결하여 좋은 성능을 낸 논문이다.
DQN이 해결한 3가지 문제.
1) Sensory input을 RL agent에 적용.
기존에는 차원의 저주 때문에 이미지나 시그널 등의 데이터를 RL에 사용하기 어려웠다. 하지만 DQN이 나오기 전 AlexNet과 같은 잘 작동하는 CNN이 등장한 때라 이 문제를 해결할 수 있었다.
2) Experience replay를 활용해 샘플 간 시간적 연관성을 줄임.
MDP는 순차적으로 진행이 되고, 최근의 경험들은 서로 연관성을 가질 수밖에 없는 문제가 있다. 이를 해결하기 위해 batch단위로 업데이트하는 방법을 제시했는데, 이 방법을 experience replay라고 한다. 당연히 여러 경험(데이터)을 가지고 업데이트하는 것이 훨씬 안정적으로 훈련될 수밖에 없다.
Experience replay는 replay buffer (memory, buffer 등으로도 불린다)라고 불리는 큐(queue)에 최근의 경험(s, a, r, s')을 저장하여 사용한다. 큐를 사용하므로 정해진 데이터 양이 쌓인 순간부터 오래된 샘플은 버리게 된다.
Experience replay는 배치 단위로 학습할 수 있다는 강력한 장점이 있지만 off-policy 기법에만 적용 가능하다는 한계가 잇다. 그러므로 REINFORCE 알고리즘을 사용한 정책 업데이트나 SARSA 같은 on-policy 방법에는 적용이 불가능하다. Target이 되는 $r+\gamma Q(s', a')$과 학습하는 $Q(s, a)$가 있을 때, off policy는 target에 사용되는 정책(Q)이 독립이라 미리 저장해 둔 s, a, r, s'을 사용가능한 반면, on policy는 target을 만들 때 정책과 학습할 때 정책이 같아서 정책을 업데이트하면 바뀌어 버려 사용이 불가능하기 때문이다.
3) Target network 도입으로 moving target 문제 해결.
함수를 근사하여 사용하지 않는 Q-learning은 특정한 Q(s, a) 업데이트가 다른 Q(s, a)에 영향을 미치지 않지만, Neual network를 사용하는 방법과 같은 함수 근사 방법은 업데이트를 하면 파라미터가 바뀌어 버려 다른 Q(s, a)에도 영향을 줄 수밖에 없게 된다. 이렇게 되면 학습하는 함수 자체를 target으로 사용하는 강화학습 특성상 target이 움직여버리는 이슈가 생긴다. 이를 해결하기 위해 DQN에서는 'target network'라는 아이디어를 제시한다. 원래 네트워크를 복사해서 일정 업데이트 동안 그대로 유지하여 타깃으로 사용하는 것이다(당연히 일정 업데이트 이후에는 다시 원래 네트워크를 복사해서 사용). 매우 간단한 아이디어인데 잘 되는 방법인 듯하다. 하지만 이 또한 일정 업데이트 이후 타깃 네트워크가 바뀌어 버리므로 학습이 불안정할 가능성이 있는 방법이긴 하다.
Double DQN ([3])
Double DQN은 maximization bias를 완화하기 위해 나온 논문이다. Neural network를 쓰기 전에 나온 Double Q-learning의 아이디어를 가져왔다.

Maximization bias 문제는 Q-learning 자체의 overestimation bias와 function approximation 오류로 인해 생긴다고 한다. 이를 해결하기 위해 타깃과 업데이트를 하는 함수를 따로 사용하는 방법이다. (Double DQN에서는 target network를 origin network에서 일정 주기마다 복사하여 사용한다.)
위의 알고리즘을 보면 $Q^{A}$를 업데이트 할 때, a*는 여전히 $Q^{A}$에서 가져오지만 그에 대한 평가는 $Q^{B}$를 사용하여 타깃을 구한다. (이는 DQN에서 봤던 target network를 사용하는 것과 비슷해 보이는데 사실 다르다. target network는 a*와 평가를 모두 $Q^{B}$가 하는 형태이다.)

Fig2를 보면 일반적인 Q-learning은 overestimation을 하고, Double Q-learning은 훨씬 덜한 것을 볼 수 있다. 이런 간단한 알고리즘이 문제를 많이 완화하여 주는 것으로 보인다.
Prioritized Replay
Replay buffer에서 experience를 샘플링할 때 가중치를 주는 아이디어이다. 가중치는 벨만 에러가 높으면 크게 주고, 낮으면 작게 주는 방식이다. $$ Bellman error = r_{i}+\gamma max_{a'} Q_{\theta} (s'_{i}, a') - Q_{\theta} (s_{i}, a_{i}) $$
Dueling Network

Dueling network는 fig 3의 위의 그림처럼 한 번에 $Q(s, a)$를 구했던 것을, 아래처럼 $V(s)+A(s, a)$로 나누어서 구하기 위해 구조를 만든 방법이다. $Q(s, a)$를 학습했을 때는 특정 state에서 하나의 action에 대해 Q-value를 얻으면 그 값에 대해서만 업데이트가 되고 다른 action에 대해서는 업데이트가 되지 않았다(NN이기 때문에 실제로는 영향을 미치긴 함). 하지만 V(s)를 학습하게 되며 동일한 state의 다른 action에 대해서도 간접적으로 학습을 할 수 있게 한다.
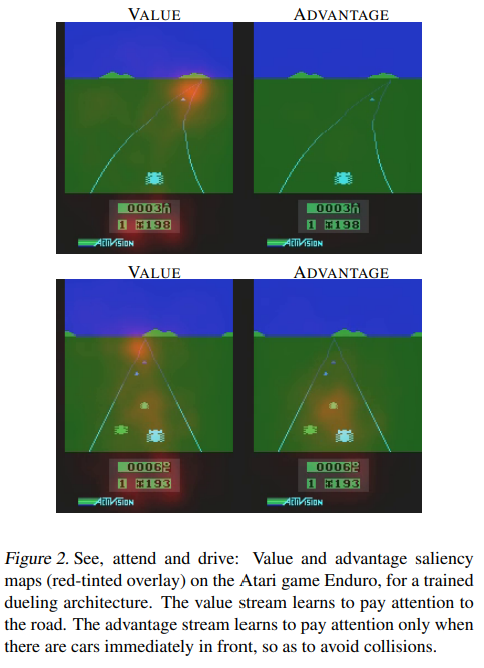
또한 fig 4의 위 그림같이 행동이 환경에 영향을 주지 않는(장애물이 없어 행동이 영향이 없음) 경우 state를 학습하는데 유용하다. Fig 4 아래 그림은 장애물이 있어 Advantage 함수가 활성화됨을 볼 수 있다.
하지만 $ Q(s,a;\theta, \alpha, \beta)$를 $V(s; \theta, \alpha) + A(s, a; \theta, \beta)$ 로 유일하게 분해할 수 없는 문제가 있다. 이를 위해 기준점을 정해놓아야 한다. 이를 위해 $ Q(s,a;\theta, \alpha, \beta) $ = $ V(s; \theta, \alpha)$ + $A(s,a; \theta, \beta) - max_{a'} A(s,a;\theta, \beta)$로 변형하면, a*=$argmax_{a' \in \mathit{A}} Q(s,a')$일 때 $Q(s,a^{*};\theta, \alpha, \beta)=V(s;\theta,\beta)$ 이므로, a*에 대해 $A(s,a; \theta, \beta) - max_{a'} A(s,a;\theta, \beta)$가 0이 되어 고정할 수 있게 된다(유일하게 분해가능!). 논문에서는 max를 사용하진 않고 mean을 사용하는데(Advantage net의 output들에 대한 평균), 이는 이론적으로 덜 타당해 보이지만 max 보다 훈련을 원활하게 하기 때문이다.
Deep Deterministic Policy Gradient (DDPG([5]))
DDPG는 연속적 행동 공간에 대한 정책을 최적화하는데, 이를 위해 DQN과 Deterministic PG를 합친 방법이다. DQN 같은 Q-learning은 연속적 행동 공간을 학습시키기 어렵다. 이를 위해서 행동을 이산화 하여 행동을 엄청 쪼개던가(상태 가치 함수의 경우) input으로 행동을 받던가 해야 하는데(행동 가치 함수의 경우), 전자의 경우는 이산화를 많이 해도 (연속 공간이므로) 최적 정책을 찾을 수 없고 비효율 적이다. 후자는 Q-learning target 계산에 필요한 $max_{a'} Q_{\theta} (s', a')$를 찾는 것이 매우 힘들다. $Q_{\theta}(s', a')$이 보통 a'에 대해 볼록 함수가 아니기 때문이다(non-convex). 그러므로 연속적 정책 함수 $\pi(a|s)$를 사용하여 Q를 학습하는 방법인 Actor-critic을 사용하게 된다. 다만 여기서 정책 함수는 deterministic 하다는 특징을 갖는다. 그 이유는 deterministic 한 정책 함수는 Q(s, a)의 기댓값 계산 시 정책이 영향을 끼치지 않아서 Q(critic)를 학습할 때 off-policy 학습이 가능하기 때문이다(replay buffer 사용 가능!). 또한 cost 함수 계산 시에도 정책에 대한 expectation이 필요 없어져서 추산치에 대한 variance가 줄어들기도 한다.
off-policy로 학습하게 되었으니 행동 정책을 선택해야 한다. 여기서는 Ornstein-Uhlenbeck 과정을 이용한다. 이는 시간적으로 서로 연관된 확률 변수를 생성하고, langevin equation 형태는 다음과 같다.
$$ \frac {dx_{t}} {dt} = -\theta x_{t} + \sigma \eta(t) $$
$\eta (t)$: white noise 과정
이는 시간적으로 연관된 확률 변수를 이용하므로 episode별로 따로 이용해야 한다. Ornstein-Uhlenbeck 과정을 코드로 표현하면 다음과 같다.
class OrnsteinUhlenbeckProcess:
def __init__(self, mu):
self.theta, self.dt, self.sigma = 0.1, 0.01, 0.1
self.mu = mu
self.x_prev = np.zeros_like(self.mu)
def __call__(self):
x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
self.x_prev = x
return x또한 논문에서는 soft-target update를 사용하는데, 기존 DQN에서 moving target issue를 해결하기 위해 도입한 target network를 한 번에 업데이트하는 것이 아니라 조금씩 업데이트해 나가는 방법이다.
Ref
[1] https://arxiv.org/abs/1312.5602
Playing Atari with Deep Reinforcement Learning
We present the first deep learning model to successfully learn control policies directly from high-dimensional sensory input using reinforcement learning. The model is a convolutional neural network, trained with a variant of Q-learning, whose input is raw
arxiv.org
[3] https://arxiv.org/abs/1509.06461
Deep Reinforcement Learning with Double Q-learning
The popular Q-learning algorithm is known to overestimate action values under certain conditions. It was not previously known whether, in practice, such overestimations are common, whether they harm performance, and whether they can generally be prevented.
arxiv.org
[4] https://arxiv.org/abs/1511.06581
Dueling Network Architectures for Deep Reinforcement Learning
In recent years there have been many successes of using deep representations in reinforcement learning. Still, many of these applications use conventional architectures, such as convolutional networks, LSTMs, or auto-encoders. In this paper, we present a n
arxiv.org
[5] https://arxiv.org/abs/1509.02971
Continuous control with deep reinforcement learning
We adapt the ideas underlying the success of Deep Q-Learning to the continuous action domain. We present an actor-critic, model-free algorithm based on the deterministic policy gradient that can operate over continuous action spaces. Using the same learnin
arxiv.org
'머신러닝&딥러닝 > 강화학습' 카테고리의 다른 글
| PPO paper 리뷰 (1) | 2023.12.13 |
|---|---|
| TD3 paper 리뷰 (0) | 2023.12.11 |
| RL 기초 개념 정리 (0) | 2023.11.24 |
| 강화학습 기초 다지기 (2) - 강화학습 문제 풀이 기법 (DP, MC, TD) (0) | 2022.05.08 |
| 강화학습 기초 다지기 (1) - 마르코프 (0) | 2022.05.01 |