Intro
일반적으로 딥러닝에서 mask는 pruning시에 사용하게 된다. 예를 들어 Lottery ticket hypothesis([1])의 경우 훈련을 마친 모델 파라미터의 magnitude를 기준으로 mask를 생성한다. 일정 값보다 작은 파라미터는 0, 나머지는 1인 mask가 생성된다. 다른 많은 pruning 방법에서도 binary mask를 생성하는 방식을 따른다. Mask는 pruning 뿐 아니라 다양한 task에서 사용되는데, 이번 글에서 그와 관련된 논문들에 대해 간단히 정리해보고자 한다.
Mask is all you need
Intro에서 언급한 것과 같이 mask는 pruning에서 많이 사용된다. Pruning에서 mask가 어떤 역할을 하는지 Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask([3])에서 나오는데, 특히 이 논문에서는 supermask라는 흥미로운 개념이 등장한다. Supermask는 모델을 학습시키지 않은 상태(init)에서 mask만 씌웠을 때 좋은 성능을 내도록 만드는 mask를 일컫는 용어다. 논문에서는 lottery ticket hypothesis의 방법을 이용해 구한 magnitude based mask를 initialize에 씌워도 원래의 initialize 모델보다 좋은 성능을 낸다는 것을 보여준다. 거기에 더해 모델은 그대로 두고 mask를 학습시키는 방법으로 모델을 학습시킬 때와 비슷한 성능을 낸다는 것을 보여준다. 이는 후속 논문 Proving the Lottery Ticket Hypothesis: Pruning is All You Need([5]) 에서 증명된다. 적당한 조건을 만족하는 (over-parameterized, bounded weights 등) network에서는 weight를 optimize 하는 것과 pruning을 하는 것이 유사하다는 내용이다.
Continual learning, Transfer learning, Meta learning, Uncertainty estimation

Super mask는 initial network만으로 좋은 성능을 내도록 만들어 준다는 강력한 특징을 가진다. 이를 이용하여 Supermasks in Superposition([2])에서는 continual learning에 적용한다. 기본이 되는 initial base network가 있고 supermasks를 implicitly 저장하고 있는 hopfield network가 있다. Hopfield network는 새로운 task가 주어졌을 때 output entropy가 작은 mask를 찾아준다. Mask를 이용한 다른 continual learning 방법으로 Pack-Net([6])이 있다.

Package network를 나타내는 말로 여러 task를 network 하나에 packaging 한다는 의미다. 학습 방법은 간단한데, 특정 task를 훈련한 모델에서 중요하지 않은(magnitude가 작은) parameter를 pruning 하고 재학습한 후, new task를 학습시켜가는 방식이다. 이렇게 되면 old task, new task를 어느 정도 잘 맞출 수 있게 된다. 이 아이디어로 transfer learning에 적용한 PAC-net: a model pruning approach to inductive transfer learning([7])도 있다. 논문의 제목처럼 pretrained data에서 배운 prior knowledge를 유지하며 transfer learning 하려고 할 때 좋은 성능을 낸다.
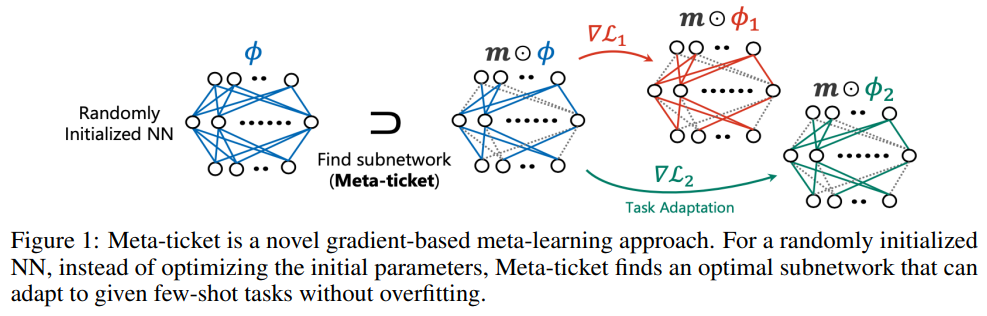
한편 Meta-ticket([8])에서는 기존 MAML 방식에서 mask를 사용하는 방법을 도입하여 meta-learning을 수행한다. Randomly intialized neural network에서 각 task별 mask를 만들어 sub-network(ticket)을 찾는 방식이다. 기본 MAML 보다는 잘 되지만, 2022년 논문임을 감안하면 성능이 엄청 좋진 않은 듯하다.
Mask는 uncertainty estimates에도 사용된다. 보통 uncertainty estimation에서 baseline으로 이용되는 방법은 ensemble([11])이다. 또한 MC-dropout([10])도 많이 사용되는데 mask를 이용한 방법이다. Ensemble은 좋은 성능을 보여주지만 학습을 여러 번 해야 한다는 치명적 단점이 존재한다. 한편 MC-dropout은 훈련을 한 번만 해도 되지만 성능이 좋지 못하다. 그 이유는 MC-dropout시 사용되는 mask들이 overlap 되는 부분이 많아 예측 값의 correlation이 높아서라고 알려져 있다. Ensemble은 서로 다른 initialize에서 시작하여 훈련하므로 다양한 inference 결과 값을 내놓기 때문에 좋은 성능을 낸다. 그래서 mask를 사용하되 overlap 되는 부분을 조절하는 방법을 제시한 Mask ensembles for uncertainty estimation([9]) 논문도 존재한다.
References
[1] https://arxiv.org/abs/1803.03635
The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
Neural network pruning techniques can reduce the parameter counts of trained networks by over 90%, decreasing storage requirements and improving computational performance of inference without compromising accuracy. However, contemporary experience is that
arxiv.org
[2] https://arxiv.org/abs/2006.14769
Supermasks in Superposition
We present the Supermasks in Superposition (SupSup) model, capable of sequentially learning thousands of tasks without catastrophic forgetting. Our approach uses a randomly initialized, fixed base network and for each task finds a subnetwork (supermask) th
arxiv.org
[3] https://arxiv.org/abs/1905.01067
Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask
The recent "Lottery Ticket Hypothesis" paper by Frankle & Carbin showed that a simple approach to creating sparse networks (keeping the large weights) results in models that are trainable from scratch, but only when starting from the same initial weights.
arxiv.org
[4] https://arxiv.org/abs/1911.13299
What's Hidden in a Randomly Weighted Neural Network?
Training a neural network is synonymous with learning the values of the weights. By contrast, we demonstrate that randomly weighted neural networks contain subnetworks which achieve impressive performance without ever training the weight values. Hidden in
arxiv.org
[5] https://arxiv.org/abs/2002.00585
Proving the Lottery Ticket Hypothesis: Pruning is All You Need
The lottery ticket hypothesis (Frankle and Carbin, 2018), states that a randomly-initialized network contains a small subnetwork such that, when trained in isolation, can compete with the performance of the original network. We prove an even stronger hypot
arxiv.org
[6] https://arxiv.org/abs/1711.05769
PackNet: Adding Multiple Tasks to a Single Network by Iterative Pruning
This paper presents a method for adding multiple tasks to a single deep neural network while avoiding catastrophic forgetting. Inspired by network pruning techniques, we exploit redundancies in large deep networks to free up parameters that can then be emp
arxiv.org
[7] https://arxiv.org/abs/2206.05703
PAC-Net: A Model Pruning Approach to Inductive Transfer Learning
Inductive transfer learning aims to learn from a small amount of training data for the target task by utilizing a pre-trained model from the source task. Most strategies that involve large-scale deep learning models adopt initialization with the pre-traine
arxiv.org
[8] https://arxiv.org/pdf/2205.15619.pdf
[9] https://arxiv.org/abs/2012.08334
Masksembles for Uncertainty Estimation
Deep neural networks have amply demonstrated their prowess but estimating the reliability of their predictions remains challenging. Deep Ensembles are widely considered as being one of the best methods for generating uncertainty estimates but are very expe
arxiv.org
[10] https://arxiv.org/abs/1506.02142
Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning
Deep learning tools have gained tremendous attention in applied machine learning. However such tools for regression and classification do not capture model uncertainty. In comparison, Bayesian models offer a mathematically grounded framework to reason abou
arxiv.org
[11] https://arxiv.org/abs/1612.01474
Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles
Deep neural networks (NNs) are powerful black box predictors that have recently achieved impressive performance on a wide spectrum of tasks. Quantifying predictive uncertainty in NNs is a challenging and yet unsolved problem. Bayesian NNs, which learn a di
arxiv.org
'머신러닝&딥러닝 > 논문리뷰' 카테고리의 다른 글
| Image Foundation Model & Transfer methods (0) | 2023.05.02 |
|---|---|
| Lottery ticket hypothesis 와 후속 연구 정리 (0) | 2022.11.27 |
| Neural Tangent Kernel 리뷰 (0) | 2022.06.12 |
| 논문 리뷰: BatchEnsemble: An Alternative Approach to Efficient Ensemble and Lifelong Learning (0) | 2021.10.16 |
| 논문 리뷰: Bayesian Meta-Learning for the Few-Shot Setting via Deep Kernels (0) | 2021.10.11 |