이 글은 graph neural network의 원리를 이해하고 앞으로 공부해나가는데 도움을 주기 위한 목적으로 작성되었습니다. 그러므로 너무 상세한 내용은 제거하고 전체적인 구조를 이해하는데 초점을 뒀습니다.
Graph
그래프는 많은 데이터가 가지고 있는 구조이다. 대표적으로 social graph, molecular graph 등이 있다. figure 1처럼 여러 개의 node(혹은 vertex)와 edge가 연결되어 있는 구조를 말한다. social graph 라면 node가 한 명의 사람이 될 수 있을 것이고 edge는 그 사이의 관계가 될 수 있다.

사람들은 각자의 개성을 가지고 있고 다르므로 node에 이런 정보를 담을 수 있으며 다른 사람과의 관계 또한 직장 동료, 친구, 가족, 원수지간까지 다양할 것이다. 이러한 정보는 edge에 담을 수 있다. 이렇게 정보를 담은 graph는 어떻게 나타내며 neural network에서는 어떻게 쓸까? 이에 대한 내용을 알아볼 것이다.
Adjacency Matrix & Feature Matrix

Figure 2와 같은 간단한 그래프 구조가 있다고 생각해 본다. 이런 구조를 matrix로 표현할 때 node 간의 관계(edge)를 표현하는 adjacency matrix와 node에 담긴 정보를 나타내는 feature matrix가 필요하다.
$$ Adjacency \; matrix \; A = \left [ \begin {matrix} 0&1&0&0 \\ 1&0&1&1 \\ 0&1&0&0 \\ 0&1&0&0 \\ \end {matrix} \right] $$
$$ Feature \; matrix \; F = \left [ \begin {matrix} 0&1&1 \\ 1&0&1 \\ 1&0&1 \\ 0&1&1 \end {matrix} \right] $$
Adjacency matrix A의 각 성분 $A_{i, j}$는 i번째 node와 j번째 node가 연결되어 있는지를 보여준다. 연결되어 있다면 1, 아니라면 0으로 숫자를 가진다. 따라서 A는 node 개수만큼의 row(행)과 column(열)을 가지는 matrix이다.
- 위와 같은 graph는 edge에 방향이 있지 않아서 undirected graph라고 하며 adjacency matrix는 symmetric 하다.
- edge에 방향이 있는 경우는 directed graph라고 하며 adjacency matrix가 symmetric 하지 않은 형태다. (예를 들어 1->2로 연결된 edge라면 1행 2열은 1의 값을 갖지만 2행 1열은 0의 값을 갖도록 표시해준다.)
Feature matrix F의 각 성분 $F_{i, j}$는 i번째 node의 j번째 feature는 무엇인지 보여준다. 여기서는 1번 node와 4번 node가 같은 색이고 2번 node와 3번 node가 같은 색이므로 같은 feature를 가졌다고 생각하여 행렬을 표현하였다. 각 node는 feature를 3개 가지고 있다고 가정하여 column(열)은 3개이며 node는 총 4개이므로 row(행)가 4개인 구조의 matrix를 가진다.
Graph Convolution Network (GCN)
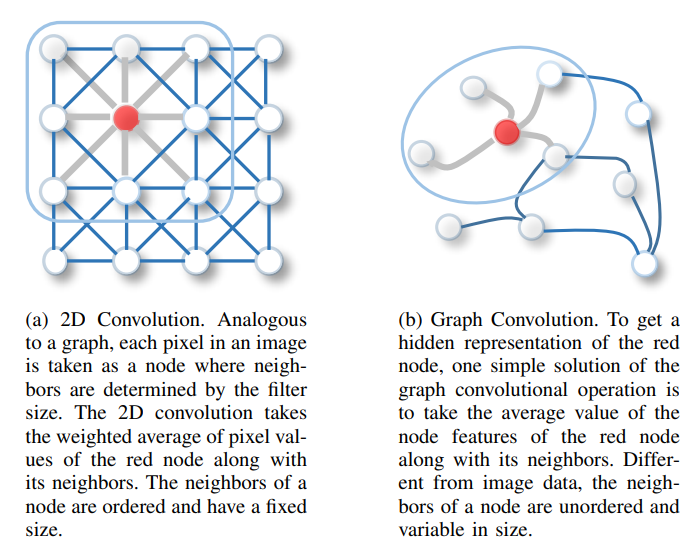
Graph structure를 matrix로 표현하는 방법을 간단히 알아보았다. Graph는 edge가 node 간의 연결을 이루는 구조이므로 edge로 연결된 node끼리의 정보 교환이 중요하다 할 수 있다. 예를 들어 social graph의 경우 서로 연결된 가족이라면 비슷한 정보를 가지고 있을 수 있고 어떤 예측을 하는데 서로 도움이 될 수 있다. 이를 위해 graph structure를 고려하여 연산을 하는 방법이 필요한데 그중 하나가 convolution을 이용한 방법이다. Figure 3 (a)를 보면 정배열된 node 간의 정보를 spatial 하게 얻어서 사용하는 방법이 convolution이고 이런 특성 때문에 Image 계열에서 많이 사용된다. 대표적인 특징으로 3가지가 있다.
- Spatial feature extraction : 주변 node의 정보를 가져와 feature를 추출한다.
- Weight Sharing : weight를 각 영역별로 따로 사용하는 게 아니라 공유하여 사용한다.
- Translation invariance : image의 경우 그림을 조금 shift 하더라도 같은 결과를 가져오게 한다.
이런 특성을 가져와 figure 3 (b)처럼 그래프에서도 주변 node의 정보를 spatial 하게 얻어 정보를 업데이트하는 방법을 고안한 것이 graph convolution network다. Figure 1의 경우에 대입해서 생각해보면 2번 node를 업데이트할 때는 1,3,4 node를 사용하지만 다른 node는 2번 node만을 사용하는 것이다. (실제로는 자기 자신의 정보도 중요하므로 자신의 정보도 함께 사용하여 업데이트한다. 즉 adjacency matrix의 대각 성분은 1이 된다.) 실제 연산은 $AFW$ matrix 연산으로 이루어진다. A는 adjacency matrix이며 F는 feature matrix, W는 weight matrix이다.
$$ F_{2}^{l+1} = \sigma(F_{1}^{l} W^{l} + F_{2} W^{l} + F_{3}^{l} W^{l} + F_{4}^{l} W^{l}) $$
위의 식은 l+1 번째 layer를 통과한 2번째 row(node)의 vector를 나타낸 것이다. $\sigma$는 activation funciton을 나타낸다. Weight matrix는 sharing 하여 모든 feature vector 연산에서 똑같이 적용된다. 예시에서는 2번째 node를 업데이트하므로 1,2,3,4 node를 모두 이용하여 업데이트하게 된다. 1번째 node였다면 1,2 node만을 이용해서 업데이트를 해야 한다. F와 W만을 이용해서는 이런 spatial 한 feature를 뽑지는 못하여 adjacency matrix A를 사용한다. Weight sharing을 사용해 업데이트된 matrix와 adjacency matrix를 연산하게 되면 각 node에 연결된 node의 feature 만을 이용하여 다음 업데이트를 하게 된다.

예를 들어 figure 2의 graph를 업데이트한다 했을 때 figure 4와 같이 matrix가 연산된다. A는 $4 \times 4$, F는 $4 \times 3$, W는 $3 \times 64$ 의 matrix를 가진다고 하겠다. $FW$를 연산하면 $4 \times 64$의 matrix가 되고 이는 각 node의 feature가 64 dimension으로 커져 고차원의 정보를 가지고 있다고 생각할 수 있다. 이 matrix와 A를 연산하면 $4 \times 64$의 matix가 되고 이 과정에서 연결된 node의 정보만을 가져와서 다시 업데이트하는 과정을 거치는 것이다. 마지막으로 graph structure로 연산을 끝낸 값을 node-wise summation을 해도 permutation invariance 하다고 한다. GCN은 convolution이 가지고 있는 특징들을 가지고 있어 graph 연산에서 강력한 이점을 가지고 있다.
추가로 adjacency matrix와 weight matrix를 여러 번 반복해서 사용하게 되면 직접 연결된 node의 정보뿐 아니라 건너 건너 연결된 node의 정보까지 이용할 수 있다. 예를 들어 figure 2의 graph 구조를 연산할 때, 첫 번째 연산에서 2번 node는 1,2,3,4 node를 이용하여 정보를 업데이트했을 것이다. 그다음 연산을 한번 더할 때 1번 node를 업데이트하기 위해 2번 node의 정보를 가져와서 사용한다면 그 node의 정보에는 기존에 업데이트된 1,2,3,4 node의 정보가 담겨 있을 것이기 때문에 1번 node와 직접 연결되지 않은 node의 정보도 이용할 수 있게 된다. 이런 식으로 여러 번 반복하면 convolution처럼 receptive field가 커지는 효과를 얻을 수 있다.
Graph pooling & message passing
Graph neural network에도 정보를 업데이트하기 위한 다양한 방법이 있다. 그중 pooling과 message passing을 간단히 알아보겠다.
Graph pooling
Pooing은 convolution neural network에서도 많이 쓰이는 방법이다. 보통 max pooling이나 average pooling을 많이 사용한다. 이름처럼 뽑은 feature에서 max값만 뽑거나 평균을 내어서 low dimension으로 만드는 방법이다. Graph pooling도 비슷하다. Figure 5의 그림과 같이 복잡한 구조의 graph structure를 단순하게 만드는 데 사용할 수 있다. CNN처럼 max값을 추출하거나 average 값을 추출할 수 있다.

한편 graph pooling은 edge나 node의 정보를 서로 전달하고자 할 때도 사용할 수 있다([2]). Social graph를 예로 들어 보겠다. 각각의 사람들에 대한 정보가 node에 담겨 있고 edge로 node가 연결되어 있다고 할 때, 사람들의 정보를 보고 관계가 좋은지 나쁜지 binary classification (edge prediction)을 하고 싶다고 해보겠다. 이때 pooling을 이용하여 다음의 단계로 prediction을 수행할 수 있다.
1. Edge별로 연결된 node의 정보(features)를 모은다.
2. 정보(features)를 합쳐서 edge로 보낸다. (pooling)
3. Parameter를 이용해서 classification을 수행한다.
이렇게 edge prediction 뿐 아니라 node prediction, global prediction도 가능하다.
Message passing
Message passing은 node 혹은 edge 간의 연관성을 고려하면서 feature를 업데이트하기 위한 방법이다([2], [4]). 예를 들어 node를 주변 node 정보를 이용해서 업데이트하고 싶을 때 message passing은 다음과 같이 이루어진다.
1. Edge로 연결되어 있는 node의 정보(features, messages)를 모은다.
2. 모든 정보를 aggregate function (sum, average 등)을 이용하여 합친다.
3. Update function(parameter)을 이용해서 새로운 정보로 업데이트한다.
Message passing을 여러 번 반복하여 receptive field를 넓힐 수 있고 더 좋은 representation을 얻을 수 있다.
간단히 graph neural network에 대한 기초 내용들을 정리해보았다. GNN은 추천 시스템, 분자구조 예측 등에서 사용된다고 알고 있다. 그 외에도 graph로 이루어진 데이터는 무수히 많고 다양한 영역에서 사용될 수 있는 잠재력이 많은 방법이라고 생각한다.
Reference
[1] https://arxiv.org/abs/1901.00596
A Comprehensive Survey on Graph Neural Networks
Deep learning has revolutionized many machine learning tasks in recent years, ranging from image classification and video processing to speech recognition and natural language understanding. The data in these tasks are typically represented in the Euclidea
arxiv.org
[2] https://distill.pub/2021/gnn-intro/
A Gentle Introduction to Graph Neural Networks
What components are needed for building learning algorithms that leverage the structure and properties of graphs?
distill.pub
[3] https://arxiv.org/abs/2012.05716
Utilising Graph Machine Learning within Drug Discovery and Development
Graph Machine Learning (GML) is receiving growing interest within the pharmaceutical and biotechnology industries for its ability to model biomolecular structures, the functional relationships between them, and integrate multi-omic datasets - amongst other
arxiv.org
[4] https://arxiv.org/pdf/1704.01212.pdf
'머신러닝&딥러닝 > 기초정리' 카테고리의 다른 글
| 데이터를 수식으로 변경! Symbolic Regression 이란? (0) | 2023.08.15 |
|---|---|
| 다양한 Hyperparameter Optimization 방법 리뷰 (1) | 2022.03.12 |
| Neural Network Pruning - 모델 경량화 (2) | 2022.02.24 |
| Multi-task learning & Meta-learning (0) | 2021.09.23 |
| Likelihood, Maximum likelihood estimation 이란? (0) | 2021.08.29 |