"A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction"(2017) - Yao Qin et al.
https://dacon.io/competitions/official/235584/overview/
이번 글에서는 Attention 기법을 Encoder와 Decoder에서 두 번 사용하는 Dual-Stage Attention 기반의 RNN을 이해하고 구현해 볼 것이다. 참고한 논문에서는 주가 데이터를 이용하여 모델을 사용하였지만 여기서는 Dacon에서 주관하는 온도 추정 경진대회의 데이터를 사용하였다.
데이터 설명
온도 추정에 사용되는 변수는 40가지이며 각각의 데이터는 다음과 같은 8개의 분류로 5개씩 존재한다.
- X00, X07, X28, X31, X32 기온
- X01, X06, X22, X27, X29 현지 기압
- X02, X03, X18, X24, X26 풍속
- X04, X10, X21, X36, X39 일일 누적강수량
- X05, X08, X09, X23, X33 해면기압
- X11, X14, X16, X19, X34 일일 누적 일사량
- X12, X20, X30, X37, X38 습도
- X13, X15, X17, X25, X35 풍향
각 분류별 데이터는 각기 다른 지역에서의 측정값을 나타낸다.(자세한 설명은 dacon 홈페이지 참고) 최종적으로 알아내고자 하는 특정지역의 온도 값을 예측하는 것이 목표다.
* hyperparameter
n: encoder input data number
m: encoder lstm features
p: decoder lstm features
T: time series length
encoder input data shape = (batch size, T, n)
decoder input data shape = (batch size, T-1, 1)
output data = (batch size) # regression 수행
모델 구조
모델의 전체 구조는 Input Attention + Encoder + Decoder로 이루어져 있다. Input Attention에서 여러 외생 변수들 사이에서 Encoder hidden state를 이용하여 중요한 Feature를 뽑아낸다. 그렇게 뽑은 데이터를 Encoder의 input으로 사용한다. Enocder의 hidden state를 update 할 때도 Decoder의 hidden state를 사용한다.
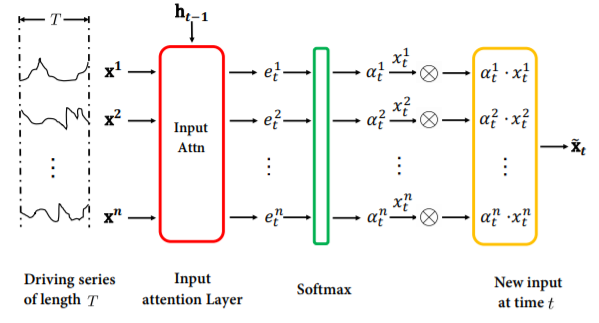
1. Input attention
Input attention의 구조는 아래 그림과 같다.
Encoder에서 사용되는 Input Attention은 예측하고자 하는 변수에 영향을 끼치는 외생변수들 중에 의미 있는 변수들에 attention 하여 사용하기 위해 적용된다. 각각 T의 시간 길이를 갖는 n개의 데이터를 사용하고 이를 Encoder에 있는 LSTM에 넣어줘서 hidden state를 뽑아준다. 코드로 구현하면 아래와 같다. (논문에서 제시한 것과 같이 hidden state와 cell state를 모두 사용하여 badahbahdanau attention을 수행한다.)
class InputAttention(Layer):
def __init__(self, T):
super(InputAttention, self).__init__(name="input_attention")
self.w1 = Dense(T)
self.w2 = Dense(T)
self.v = Dense(1)
def call(self, h_s, c_s, x):
"""
h_s : hidden_state (shape = batch,m)
c_s : cell_state (shape = batch,m)
x : time series encoder inputs (shape = batch,T,n)
"""
query = tf.concat([h_s, c_s], axis=-1) # batch, m*2
query = RepeatVector(x.shape[2])(query) # batch, n, m*2
x_perm = Permute((2, 1))(x) # batch, n, T
score = tf.nn.tanh(self.w1(x_perm) + self.w2(query)) # batch, n, T
score = self.v(score) # batch, n, 1
score = Permute((2, 1))(score) # batch,1,n
attention_weights = tf.nn.softmax(score) # t 번째 time step 일 때 각 feature 별 중요도
return attention_weights
2. Encoder
모든 time step에 대해 attention weights를 구해준것을 받으면 input data와 곱해줘서 $\hat {x}_{t}$를 구해준다. 코드로 구현하면 다음과 같다.
class Encoderlstm(Layer):
def __init__(self, m):
"""
m : feature dimension
h0 : initial hidden state
c0 : initial cell state
"""
super(Encoderlstm, self).__init__(name="encoder_lstm")
self.lstm = LSTM(m, return_state=True)
self.initial_state = None
def call(self, x, training=False):
"""
x : t 번째 input data (shape = batch,1,n)
"""
h_s, _, c_s = self.lstm(x, initial_state=self.initial_state)
self.initial_state = [h_s, c_s]
return h_s, c_s
def reset_state(self, h0, c0):
self.initial_state = [h0, c0]
class Encoder(Layer):
def __init__(self, T, m):
super(Encoder, self).__init__(name="encoder")
self.T = T
self.input_att = InputAttention(T)
self.lstm = Encoderlstm(m)
self.initial_state = None
self.alpha_t = None
def call(self, data, h0, c0, n=39, training=False):
"""
data : encoder data (shape = batch, T, n)
n : data feature num
"""
self.lstm.reset_state(h0=h0, c0=c0)
alpha_seq = tf.TensorArray(tf.float32, self.T)
for t in range(self.T):
x = Lambda(lambda x: data[:, t, :])(data)
x = x[:, tf.newaxis, :] # (batch,1,n)
h_s, c_s = self.lstm(x)
self.alpha_t = self.input_att(h_s, c_s, data) # batch,1,n
alpha_seq = alpha_seq.write(t, self.alpha_t)
alpha_seq = tf.reshape(alpha_seq.stack(), (-1, self.T, n)) # batch, T, n
output = tf.multiply(data, alpha_seq) # batch, T, n
return output
3. Decoder
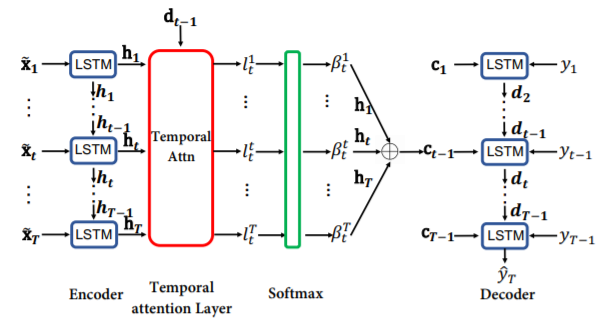
Attention 메커니즘이 적용된 변수 $\hat{x}_{t}$를 가지고 LSTM에 넣어준 후, 2번째 Attention인 Temporal attention을 적용해준다. 이 기법은 Encoder에서 얻은 모든 Time step에서의 Hidden state와 각 time step에서의 Decoder LSTM의 hidden state를 비교하여 Attention 한 Context Vector를 추출하기 위한 메커니즘이다.
이를 코드로 구현한 결과는 다음과 같다. (여기서도 마찬가지로 논문에서 제시한 대로 hidden state와 cell state를 모두 사용한다.)
class TemporalAttention(Layer):
def __init__(self, m):
super(TemporalAttention, self).__init__(name="temporal_attention")
self.w1 = Dense(m)
self.w2 = Dense(m)
self.v = Dense(1)
def call(self, h_s, c_s, enc_h):
"""
h_s : hidden_state (shape = batch,p)
c_s : cell_state (shape = batch,p)
enc_h : time series encoder inputs (shape = batch,T,m)
"""
query = tf.concat([h_s, c_s], axis=-1) # batch, p*2
query = RepeatVector(enc_h.shape[1])(query)
score = tf.nn.tanh(self.w1(enc_h) + self.w2(query)) # batch, T, m
score = self.v(score) # batch, T, 1
attention_weights = tf.nn.softmax(
score, axis=1
) # encoder hidden state h(i) 의 중요성 (0<=i<=T)
return attention_weights
$y_{t}$ 값을 예측할 때는 이전 time step에서의 실제 y값과 Context Vector를 Concatenate해준 후 Dense layer를 거쳐 출력을 낸다. 그리고 다음 Lstm에는 예측값을 넣어주며 최종 결과인 $y_{T}$ 를 내준다. 이를 코드로 구현하면 다음과 같다.
class Decoderlstm(Layer):
def __init__(self, p):
"""
p : feature dimension
h0 : initial hidden state
c0 : initial cell state
"""
super(Decoderlstm, self).__init__(name="decoder_lstm")
self.lstm = LSTM(p, return_state=True)
self.initial_state = None
def call(self, x, training=False):
"""
x : t 번째 input data (shape = batch,1,n)
"""
h_s, _, c_s = self.lstm(x, initial_state=self.initial_state)
self.initial_state = [h_s, c_s]
return h_s, c_s
def reset_state(self, h0, c0):
self.initial_state = [h0, c0]
class Decoder(Layer):
def __init__(self, T, p, m):
super(Decoder, self).__init__(name="decoder")
self.T = T
self.temp_att = TemporalAttention(m)
self.dense = Dense(1)
self.lstm = Decoderlstm(p)
self.enc_lstm_dim = m
self.dec_lstm_dim = p
self.context_v = None
self.dec_h_s = None
self.beta_t = None
def call(self, data, enc_h, h0=None, c0=None, training=False):
"""
data : decoder data (shape = batch, T-1, 1)
enc_h : encoder hidden state (shape = batch, T, m)
"""
h_s = None
self.lstm.reset_state(h0=h0, c0=c0)
self.context_v = tf.zeros((enc_h.shape[0], 1, self.enc_lstm_dim)) # batch,1,m
self.dec_h_s = tf.zeros((enc_h.shape[0], self.dec_lstm_dim)) # batch, p
for t in range(self.T - 1): # 0~T-1
x = Lambda(lambda x: data[:, t, :])(data)
x = x[:, tf.newaxis, :] # (batch,1,1)
x = tf.concat([x, self.context_v], axis=-1) # batch, 1, m+1
x = self.dense(x) # batch,1,1
h_s, c_s = self.lstm(x) # batch,p
self.beta_t = self.temp_att(h_s, c_s, enc_h) # batch, T, 1
self.context_v = tf.matmul(
self.beta_t, enc_h, transpose_a=True
) # batch,1,m
return tf.concat(
[h_s[:, tf.newaxis, :], self.context_v], axis=-1
) # batch,1,m+p
위의 Layer들을 모두 합쳐 DARNN을 생성한 코드는 다음과 같다.
class DARNN(Model):
def __init__(self, T, m, p):
super(DARNN, self).__init__(name="DARNN")
"""
T : 주기 (time series length)
m : encoder lstm feature length
p : decoder lstm feature length
h0 : lstm initial hidden state
c0 : lstm initial cell state
"""
self.m = m
self.encoder = Encoder(T=T, m=m)
self.decoder = Decoder(T=T, p=p, m=m)
self.lstm = LSTM(m, return_sequences=True)
self.dense1 = Dense(p)
self.dense2 = Dense(1)
def call(self, inputs, training=False, mask=None):
"""
inputs : [enc , dec]
enc_data : batch,T,n
dec_data : batch,T-1,1
"""
enc_data, dec_data = inputs
batch = enc_data.shape[0]
h0 = tf.zeros((batch, self.m))
c0 = tf.zeros((batch, self.m))
enc_output = self.encoder(
enc_data, n=39, h0=h0, c0=c0, training=training
) # batch, T, n
enc_h = self.lstm(enc_output) # batch, T, m
dec_output = self.decoder(
dec_data, enc_h, h0=h0, c0=c0, training=training
) # batch,1,m+p
output = self.dense2(self.dense1(dec_output))
output = tf.squeeze(output)
return output
Experimentsal reults
논문에서 주식 데이터에 대해 다른 알고리즘들과 비교했을 때 우수한 성능을 냈다. 여기서는 직접 실험한 결과를 소개한다.
test data(10000개)에 대해서 예측 값과 정답 값을 Scatter plot을 이용하여 나타낸 값이다. 튀는 값이 조금 있지만 대체적으로 선형 그래프를 나타내며 학습이 잘 된 것 같다. (사실 10분 뒤의 결과를 예측하는 것이라 어렵지 않은 task다.)

Encoder에서 각 변수들에 대한 중요도를 계산한 Alpha(encoder attention weights)를 그래프로 표현하면 아래와 같다. 대부분 비슷한 중요도를 가지는 것으로 나타난다. 그 중에서도 습도에 대한 변수들이 높은 attention value를 가지는 것을 볼 수 있다. 기온과 관련한 값들이 높을 것으로 예상하였지만 다른 결과가 나왔다.

Decoder에서 Time step별 중요도를 나타내는 Beta(decoder attention weights)를 그래프로 표현하면 다음과 같다. 다음 10분을 예측하는 것이라 그전 time step이 가장 중요한 feature가 될 것이라 예측하였으나 그렇게 나오지 않았다. 다른 지역에 대한 예측이라 그런 것인지 학습이 잘 되지 않은 것인지는 판단하기 어렵다.

전체 코드에 대한 문의가 많아 Github에 데이터 처리부터 모델 실행까지의 코드를 올려두었습니다. 추가로 colab에서 실행한 버전도 올려두었습니다.
* Attention에 사용되는 하이퍼 파라미터는 기본적으로 논문에 나온 내용을 따랐습니다.